Drug Discovery: Protein Folding on IBM’s Qiskit Quantum Information Framework : NVIDIA A100 exascale.mahidol.ac.th
Before Covid-19 there is shown of obstacles for Quantum Supremacy[7]. December 2021, simulating the sycamore quantum supremacy circuit hooked our future “optimazation algorithms” imagination[8]. After than we have worked cuQuantum but there is not progress after a year. Until we get one motivation that we can try quantum information on GPU[9]. Finally, end up with IBM’s Qiskit framework for two reasons that very youtube video and tutorial[10]. The second that Qiskit drawn our attention is “Protien folding”[11]. Having been tried on QAOA on GPUs, we are VQE is promissing.
The follo detail actually 99.9999% from the source [11] with migration to run on GPUs and cuQuantum.
Introduction
The structure and function of many natural and human-engineered proteins is still only poorly understood. As a result, our understanding of processes connected with protein folding, such as those encountered in Alzheimer’s disease, vaccine development, and crop improvement research, has remained limited.
Unfolded polypeptides have a very large number of degrees of freedom and thus an enormous number of potential conformations. For example, a chain with $100$ aminoacids has on the order of $10^{47}$ conformations. In reality, however, many proteins fold to their native structure within seconds. This is known as Levinthal’s paradox [1].
The exponential growth of potential conformations with chain length makes the problem intractable for classical computers. In the quantum framework, our resource-efficient algorithm scales linearly with the number of aminoacids N.
The goal of this work is to determine the minimum energy conformation of a protein. Starting from a random configuration, the protein’s structure is optimized to lower the energy. This can be achieved by encoding the protein folding problem into a qubit operator and ensuring that all physical constraints are satisfied.
For the problem encoding we use:
Configuration qubits: qubits that are used to describe the configurations and the relative position of the different beads
Interaction qubits: qubits that encode interactions between the different aminoacids
For our case we use a tetrahedral lattice (diamond shape lattice) where we encode the movement through the configuration qubits (see image below).
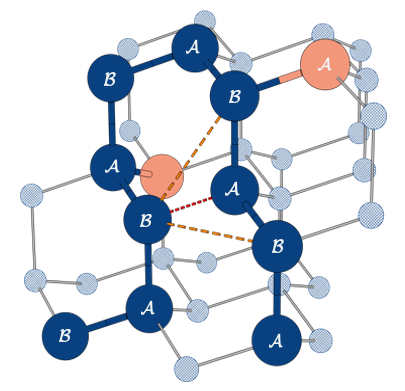
The Hamiltonian of the system for a set of qubits $\mathbf{q}={\mathbf{q}{cf}, \mathbf{q}{in}}$ is
\[H(\mathbf{q}) = H_{gc}(\mathbf{q}_{cf}) + H_{ch}(\mathbf{q}_{cf}) + H_{in}(\mathbf{q}_{cf}, \mathbf{q}_{in})\]where
$H_{gc}$ is the geometrical constraint term (governing the growth of the primary sequence of aminoacids without bifurcations)
$H_{ch}$ is the chirality constraint (enforcing the right stereochemistry for the system)
$H_{in}$ is the interaction energy terms of the system. In our case we consider only nearest neighbor interactions.
Further details about the used model and the encoding of the problem can be found in [2].
1
2
3
4
! git clone https://github.com/qiskit-research/qiskit-research.git
! cd qiskit-research && pip install .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from qiskit_research.protein_folding.interactions.random_interaction import (
RandomInteraction,
)
from qiskit_research.protein_folding.interactions.miyazawa_jernigan_interaction import (
MiyazawaJerniganInteraction,
)
from qiskit_research.protein_folding.peptide.peptide import Peptide
from qiskit_research.protein_folding.protein_folding_problem import (
ProteinFoldingProblem,
)
from qiskit_research.protein_folding.penalty_parameters import PenaltyParameters
from qiskit.utils import algorithm_globals, QuantumInstance
algorithm_globals.random_seed = 23
Protein Main Chain
The Protein consists of a main chain that is a linear chain of aminoacids. For the naming of different residues we use the one-letter code as defined in Ref. [3]. Further details about the naming and the type of aminoacids can also be found in [4].
For this particular case we demonstrate the generation of the qubit operator in a neuropeptide with the main chain consisting of 7 aminoacids with letter codes APRLRFY (see also [2]).
1
main_chain = "APRLRFY"
Side Chains
Beyond the main chain of the protein there may be aminoacids attached to the residues of the main chain. Our model allows for side chains of the maximum length of one. Elongated side chains would require the introduction of additional penalty terms which are still under development. In this example we do not consider any side chains to keep the real structure of the neuropeptide.
1
side_chains = [""] * 7
Interaction between Aminoacids
For the description of inter-residue contacts for proteins we use knowledge-based (statistical) potentials derived using quasi-chemical approximation. The potentials used here are introduced by Miyazawa, S. and Jernigan, R. L. in [5].
Beyond this model we also allow for random contact maps (interactions) that provide a random interaction map. One can also introduce a custom interaction map that enhances certain configurations of the protein (e.g. alpha helix, beta sheet etc).
1
2
random_interaction = RandomInteraction()
mj_interaction = MiyazawaJerniganInteraction()
Physical Constraints
To ensure that all physical constraints are respected we introduce penalty functions. The different penalty terms used are:
penalty_chiral: A penalty parameter used to impose the right chirality.
penalty_back: A penalty parameter used to penalize turns along the same axis. This term is used to eliminate sequences where the same axis is chosen twice in a row. In this way we do not allow for a chain to fold back into itself.
penalty_1: A penalty parameter used to penalize local overlap between beads within a nearest neighbor contact.
1
2
3
4
5
penalty_back = 10
penalty_chiral = 10
penalty_1 = 10
penalty_terms = PenaltyParameters(penalty_chiral, penalty_back, penalty_1)
Peptide Definition
Based on the main chain and possible side chains we define the peptide object that includes all the structural information of the modeled system.
1
peptide = Peptide(main_chain, side_chains)
Protein Folding Problem
Based on the defined peptide, the interaction (contact map) and the penalty terms we defined for our model we define the protein folding problem that returns qubit operators.
1
2
protein_folding_problem = ProteinFoldingProblem(peptide, mj_interaction, penalty_terms)
qubit_op = protein_folding_problem.qubit_op()
1
print(qubit_op)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
1613.5895000000003 * IIIIIIIII
+ 487.5 * IIIIIIZII
- 192.5 * IIIIIIIZZ
+ 192.5 * IIIIIIZZZ
- 195.0 * IIIIZIZII
- 195.0 * IIIIIZIZI
- 195.0 * IIIIZZZZI
- 95.0 * IIZIZIIII
- 95.0 * IIIZIZIII
- 95.0 * IIZZZZIII
+ 295.0 * IIIIIIZZI
- 497.5 * IIIIZIIII
- 300.0 * IIIIZZIII
+ 195.0 * IIIIIIIIZ
+ 197.5 * IIIIIZIIZ
- 197.5 * IIIIZZIIZ
- 904.2875 * IZIIIIIII
- 295.0 * IZIIIIZII
- 197.5 * IZIIIIZZI
+ 302.5 * IZIIZIIII
+ 202.5 * IZIIZZIII
+ 100.0 * IZIIZIZII
+ 100.0 * IZIIIZIZI
+ 100.0 * IZIIZZZZI
- 200.0 * IZIIIIIIZ
+ 97.5 * IZIIIIIZZ
- 97.5 * IZIIIIZZZ
- 100.0 * IZIIIZIIZ
+ 100.0 * IZIIZZIIZ
+ 100.0 * IIIIIIIZI
- 100.0 * IIIIIZIII
+ 2.5 * IZIIIIIZI
- 2.5 * IZIIIZIII
+ 192.5 * IIZIIIIII
+ 95.0 * IIZZIIIII
+ 97.5 * IIZIIIZII
+ 97.5 * IIIZIIIZI
+ 97.5 * IIZZIIZZI
- 97.5 * IIIZIIIIZ
+ 97.5 * IIZZIIIIZ
+ 7.5 * IZZIIIIII
+ 5.0 * IZZZIIIII
+ 2.5 * IZZIIIZII
+ 2.5 * IZIZIIIZI
+ 2.5 * IZZZIIZZI
- 2.5 * IZZIZIIII
- 2.5 * IZIZIZIII
- 2.5 * IZZZZZIII
- 2.5 * IZIZIIIIZ
+ 2.5 * IZZZIIIIZ
+ 105.0 * IIIZIIIII
- 701.802 * ZIIIIIIII
- 195.0 * ZIIIIIZII
- 102.5 * ZIIIIIIZI
- 97.5 * ZIIIIIZZI
+ 195.0 * ZIIIZIIII
+ 102.5 * ZIIIIZIII
+ 97.5 * ZIIIZZIII
- 200.0 * ZIZIIIIII
- 105.0 * ZIIZIIIII
- 100.0 * ZIZZIIIII
+ 97.5 * ZIIIZIZII
- 100.0 * ZIZIIIZII
+ 97.5 * ZIIIIZIZI
- 100.0 * ZIIZIIIZI
+ 97.5 * ZIIIZZZZI
- 100.0 * ZIZZIIZZI
+ 100.0 * ZIZIZIIII
+ 100.0 * ZIIZIZIII
+ 100.0 * ZIZZZZIII
+ 97.5 * ZIIIIIIZZ
- 97.5 * ZIIIIIZZZ
- 97.5 * ZIIIIZIIZ
+ 97.5 * ZIIIZZIIZ
+ 100.0 * ZIIZIIIIZ
- 100.0 * ZIZZIIIIZ
+ 5.0 * ZIIIIIIIZ
Using VQE with CVaR expectation value for the solution of the problem
The problem that we are tackling has now implemented all the physical constraints and has a diagonal Hamiltonian. For the particular case we are targeting the single bitstring that gives us the minimum energy (corresponding to the folded structure of the protein). Thus, we can use the Variational Quantum Eigensolver with Conditional Value at Risk (CVaR) expectation values for the solution of the problem and for finding the minimum configuration energy [6] . We follow the same approach as in Ref. [2] but here we use COBYLA for the classical optimization part. One can also use the standard VQE or QAOA algorithm for the solution of the problem, though as discussed in Ref. [2] CVaR is more suitable.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from qiskit.circuit.library import RealAmplitudes
from qiskit.algorithms.optimizers import COBYLA
from qiskit.algorithms import NumPyMinimumEigensolver, VQE
from qiskit.opflow import PauliExpectation, CVaRExpectation
#from qiskit import execute, Aer
from qiskit.providers.aer import *
import time
# set classical optimizer
optimizer = COBYLA(maxiter=50)
# set variational ansatz
ansatz = RealAmplitudes(reps=1)
# set the backend
#backend_name = "aer_simulator" # CPU configure
#backend_name = "aer_simulator_statevector" # GPU configure
#backend_name = AerSimulator(method = 'statevector',device = 'GPU', blocking_qubits=20)
#backend_name = AerSimulator(method = 'statevector',device = 'GPU')
backend_name = AerSimulator(method = 'automatic',device = 'GPU',blocking_qubits=10)
#backend_name = AerSimulator(method = 'automatic')
#backend_name = 'qasm_simulator'
backend = QuantumInstance(
# Aer.get_backend(backend_name),
backend_name,
shots=8192,
seed_transpiler=algorithm_globals.random_seed,
seed_simulator=algorithm_globals.random_seed,
)
counts = []
values = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
# initialize CVaR_alpha objective with alpha = 0.1
cvar_exp = CVaRExpectation(0.1, PauliExpectation())
# initialize VQE using CVaR
vqe = VQE(
expectation=cvar_exp,
#expectation=None,
optimizer=optimizer,
ansatz=ansatz,
quantum_instance=backend,
callback=store_intermediate_result,
#include_custom=True, # for statevector simulatio, set True, if expectation = None
)
start = time.process_time()
raw_result = vqe.compute_minimum_eigenvalue(qubit_op)
print(time.process_time() - start)
print(raw_result)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
/home/snit.san/miniconda3/envs/Qiskit/lib/python3.10/site-packages/qiskit/algorithms/minimum_eigen_solvers/vqe.py:625: RuntimeWarning: invalid value encountered in sqrt
estimator_error = np.sqrt(variance / self.quantum_instance.run_config.shots)
22.066488650000004
{ 'aux_operator_eigenvalues': None,
'cost_function_evals': 50,
'eigenstate': { '000000101': 0.015625,
'000000110': 0.029231698334171417,
'000000111': 0.011048543456039806,
'000010000': 0.011048543456039806,
'000010101': 0.011048543456039806,
'000010110': 0.019136638615493577,
'000110110': 0.011048543456039806,
'000111000': 0.011048543456039806,
'000111001': 0.011048543456039806,
'001000000': 0.038273277230987154,
'001000001': 0.06810779599282303,
'001000010': 0.06346905003621844,
'001000011': 0.015625,
'001000101': 0.15934435979977452,
'001000110': 0.2910615001593306,
'001000111': 0.05182226234930312,
'001001000': 0.036643873123620545,
'001001001': 0.0924387466109315,
'001001010': 0.07328774624724109,
'001001100': 0.011048543456039806,
'001001101': 0.03125,
'001001110': 0.059498227389561786,
'001010000': 0.019136638615493577,
'001010001': 0.029231698334171417,
'001010010': 0.02209708691207961,
'001010011': 0.011048543456039806,
'001010100': 0.011048543456039806,
'001010101': 0.09568319307746789,
'001010110': 0.16275520824999734,
'001010111': 0.03983608994994363,
'001011001': 0.02209708691207961,
'001011010': 0.011048543456039806,
'001011100': 0.011048543456039806,
'001011101': 0.036643873123620545,
'001011110': 0.05740991584648074,
'001100001': 0.03125,
'001100010': 0.019136638615493577,
'001100101': 0.03314563036811941,
'001100110': 0.07328774624724109,
'001100111': 0.015625,
'001101000': 0.06987712429686843,
'001101001': 0.13975424859373686,
'001101010': 0.10597390598633231,
'001101011': 0.036643873123620545,
'001101101': 0.034938562148434216,
'001101110': 0.06899813176818631,
'001110000': 0.05633673867912483,
'001110001': 0.11587810136086973,
'001110010': 0.0897587913521567,
'001110011': 0.024705294220065465,
'001110101': 0.11744762795603834,
'001110110': 0.22371595411369302,
'001110111': 0.0427908248050911,
'001111000': 0.12153397801643785,
'001111001': 0.2602864257649638,
'001111010': 0.21079277442550065,
'001111011': 0.03983608994994363,
'001111101': 0.015625,
'001111110': 0.027063293868263706,
'010000001': 0.015625,
'010000010': 0.015625,
'010000101': 0.029231698334171417,
'010000110': 0.046875,
'010000111': 0.011048543456039806,
'010001000': 0.011048543456039806,
'010001001': 0.02209708691207961,
'010001010': 0.019136638615493577,
'010001110': 0.011048543456039806,
'010001111': 0.011048543456039806,
'010010001': 0.011048543456039806,
'010010101': 0.02209708691207961,
'010010110': 0.029231698334171417,
'010010111': 0.011048543456039806,
'010011110': 0.011048543456039806,
'010100101': 0.015625,
'010100110': 0.02209708691207961,
'010101000': 0.011048543456039806,
'010101001': 0.029231698334171417,
'010101010': 0.02209708691207961,
'010101101': 0.011048543456039806,
'010101110': 0.019136638615493577,
'010110000': 0.015625,
'010110001': 0.02209708691207961,
'010110010': 0.015625,
'010110101': 0.02209708691207961,
'010110110': 0.034938562148434216,
'010111000': 0.027063293868263706,
'010111001': 0.05633673867912483,
'010111010': 0.05063078670631141,
'010111011': 0.011048543456039806,
'011000101': 0.011048543456039806,
'011000110': 0.015625,
'011001010': 0.011048543456039806,
'011101010': 0.011048543456039806,
'011110110': 0.011048543456039806,
'011111001': 0.02209708691207961,
'011111010': 0.02209708691207961,
'100000001': 0.019136638615493577,
'100000100': 0.011048543456039806,
'100000101': 0.015625,
'100000110': 0.029231698334171417,
'100010010': 0.011048543456039806,
'100010101': 0.011048543456039806,
'100010110': 0.029231698334171417,
'100110010': 0.011048543456039806,
'100110110': 0.011048543456039806,
'100111001': 0.015625,
'100111010': 0.015625,
'101000000': 0.04555431167847891,
'101000001': 0.08193819126329309,
'101000010': 0.061515686515717274,
'101000011': 0.02209708691207961,
'101000100': 0.015625,
'101000101': 0.16350351200356522,
'101000110': 0.31483502624390447,
'101000111': 0.04941058844013093,
'101001000': 0.034938562148434216,
'101001001': 0.09043622580304864,
'101001010': 0.08118988160479113,
'101001011': 0.024705294220065465,
'101001101': 0.02209708691207961,
'101001110': 0.06051536478449089,
'101001111': 0.019136638615493577,
'101010000': 0.02209708691207961,
'101010001': 0.015625,
'101010010': 0.02209708691207961,
'101010101': 0.0897587913521567,
'101010110': 0.16275520824999734,
'101010111': 0.024705294220065465,
'101011010': 0.015625,
'101011100': 0.011048543456039806,
'101011101': 0.019136638615493577,
'101011110': 0.05412658773652741,
'101011111': 0.019136638615493577,
'101100000': 0.011048543456039806,
'101100001': 0.027063293868263706,
'101100010': 0.015625,
'101100101': 0.03314563036811941,
'101100110': 0.06810779599282303,
'101100111': 0.011048543456039806,
'101101000': 0.06346905003621844,
'101101001': 0.12597277731716483,
'101101010': 0.10825317547305482,
'101101011': 0.036643873123620545,
'101101101': 0.05063078670631141,
'101101110': 0.07574499777213015,
'101101111': 0.015625,
'101110000': 0.059498227389561786,
'101110001': 0.12052537984798056,
'101110010': 0.09631896879639025,
'101110011': 0.02209708691207961,
'101110101': 0.1269381000724369,
'101110110': 0.23593232610221093,
'101110111': 0.034938562148434216,
'101111000': 0.12979099785809492,
'101111001': 0.2679129406169101,
'101111010': 0.22803936748947537,
'101111011': 0.048159484398195125,
'101111100': 0.011048543456039806,
'101111101': 0.011048543456039806,
'101111110': 0.034938562148434216,
'110000010': 0.019136638615493577,
'110000101': 0.03125,
'110000110': 0.05846339666834283,
'110000111': 0.011048543456039806,
'110001001': 0.019136638615493577,
'110001010': 0.011048543456039806,
'110001110': 0.015625,
'110010001': 0.011048543456039806,
'110010101': 0.011048543456039806,
'110010110': 0.038273277230987154,
'110100010': 0.011048543456039806,
'110100011': 0.011048543456039806,
'110100100': 0.011048543456039806,
'110101000': 0.02209708691207961,
'110101001': 0.03125,
'110101010': 0.011048543456039806,
'110101110': 0.015625,
'110110001': 0.011048543456039806,
'110110010': 0.015625,
'110110101': 0.03125,
'110110110': 0.0427908248050911,
'110110111': 0.011048543456039806,
'110111000': 0.019136638615493577,
'110111001': 0.05633673867912483,
'110111010': 0.03983608994994363,
'110111110': 0.011048543456039806,
'111010110': 0.011048543456039806},
'eigenvalue': (-1.3961062011717185+0j),
'optimal_circuit': None,
'optimal_parameters': { ParameterVectorElement(θ[3]): 0.9692262567242826,
ParameterVectorElement(θ[4]): 1.2642867883228641,
ParameterVectorElement(θ[14]): 0.8463792877027871,
ParameterVectorElement(θ[16]): -0.014459268936528602,
ParameterVectorElement(θ[12]): 2.18024157641206,
ParameterVectorElement(θ[17]): -1.6753431921616952,
ParameterVectorElement(θ[15]): 3.2569738080876025,
ParameterVectorElement(θ[13]): 2.7683897737290772,
ParameterVectorElement(θ[0]): 1.2838423033219764,
ParameterVectorElement(θ[5]): 3.2075406912327287,
ParameterVectorElement(θ[7]): -3.0610226240215836,
ParameterVectorElement(θ[9]): -0.5499117056945564,
ParameterVectorElement(θ[6]): 2.758502107235997,
ParameterVectorElement(θ[11]): 1.6613895556624305,
ParameterVectorElement(θ[10]): 0.783563408369476,
ParameterVectorElement(θ[8]): 3.062947537861036,
ParameterVectorElement(θ[1]): 2.5249570586597203,
ParameterVectorElement(θ[2]): -2.0271296314251086},
'optimal_point': array([ 1.2838423 , 2.52495706, -2.02712963, 0.96922626, 1.26428679,
3.20754069, 2.75850211, -3.06102262, 3.06294754, -0.54991171,
0.78356341, 1.66138956, 2.18024158, 2.76838977, 0.84637929,
3.25697381, -0.01445927, -1.67534319]),
'optimal_value': -1.3961062011717185,
'optimizer_evals': None,
'optimizer_result': None,
'optimizer_time': 22.18771505355835}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
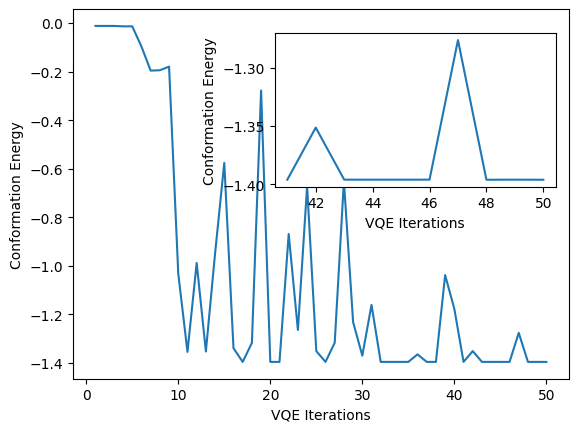
import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(counts, values)
plt.ylabel("Conformation Energy")
plt.xlabel("VQE Iterations")
fig.add_axes([0.44, 0.51, 0.44, 0.32])
plt.plot(counts[40:], values[40:])
plt.ylabel("Conformation Energy")
plt.xlabel("VQE Iterations")
plt.show()
Visualizing the answer
In order to reduce computational costs, we have reduced the problem’s qubit operator to the minimum amount of qubits needed to represent the shape of the protein. In order to decode the answer we need to understand how this has been done.
- The shape of the protein has been encoded by a sequence of turns , ${0,1,2,3}$. Each turn represents a different direction in the lattice.
- For a main bead of $N_{aminoacids}$ in a lattice, we need $N_{aminoacids}-1$ turns in order to represent its shape. However, the orientation of the protein is not relevant to its energy. Therefore the first two turns of the shape can be set to $[1,0]$ without loss of generality.
- If the second bead does not have any side chain, we can also set the $6^{th}$ qubit to $[1]$ without breaking symmetry.
- Since the length of the secondary chains is always limited to $1$ we only need one turn to describe the shape of the chain.
The total amount of qubits we need to represent the shape of the protein will be $2(N_{aminoacids}-3)$ if there is a secondary chain coming out of the second bead or $2(N_{aminoacids}-3) - 1$, otherwise. All the other qubits will remain unused during the optimization process. See:
1
2
3
4
5
6
result = protein_folding_problem.interpret(raw_result=raw_result)
print(
"The bitstring representing the shape of the protein during optimization is: ",
result.turn_sequence,
)
print("The expanded expression is:", result.get_result_binary_vector())
1
2
The bitstring representing the shape of the protein during optimization is: 101000110
The expanded expression is: 1______0_____________________________________________________________________________________________________________________________100011_0____
Now that we know which qubits encode which information, we can decode the bitstring into the explicit turns that form the shape of the protein.
1
2
3
4
print(
f"The folded protein's main sequence of turns is: {result.protein_shape_decoder.main_turns}"
)
print(f"and the side turn sequences are: {result.protein_shape_decoder.side_turns}")
1
2
The folded protein's main sequence of turns is: [1, 0, 1, 3, 0, 1]
and the side turn sequences are: [None, None, None, None, None, None, None]
From this sequence of turns we can get the cartesian coordinates of each of the aminoacids of the protein.
1
print(result.protein_shape_file_gen.get_xyz_data())
1
2
3
4
5
6
7
[['A' '0.0' '0.0' '0.0']
['P' '0.5773502691896258' '0.5773502691896258' '-0.5773502691896258']
['R' '1.1547005383792517' '0.0' '-1.1547005383792517']
['L' '1.7320508075688776' '0.5773502691896258' '-1.7320508075688776']
['R' '1.154700538379252' '1.1547005383792517' '-2.3094010767585034']
['F' '0.5773502691896261' '1.7320508075688776' '-1.7320508075688776']
['Y' '2.220446049250313e-16' '1.154700538379252' '-1.154700538379252']]
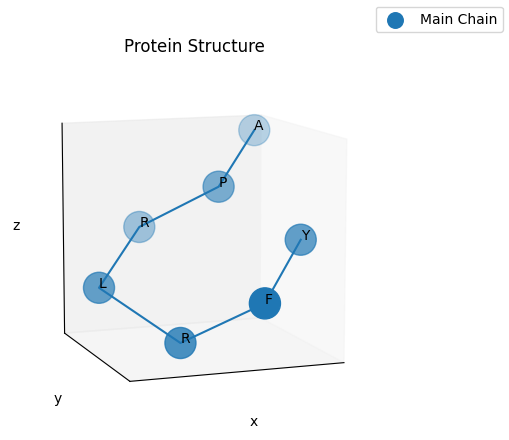
And finally, we can also plot the structure of the protein in 3D. Note that when rendered with the proper backend this plot can be interactively rotated.
1
2
fig = result.get_figure(title="Protein Structure", ticks=False, grid=True)
fig.get_axes()[0].view_init(10, 70)
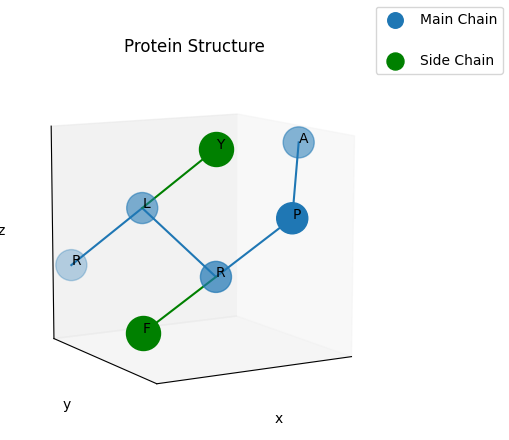
And here is an example with side chains.
1
2
3
4
5
peptide = Peptide("APRLR", ["", "", "F", "Y", ""])
protein_folding_problem = ProteinFoldingProblem(peptide, mj_interaction, penalty_terms)
qubit_op = protein_folding_problem.qubit_op()
raw_result = vqe.compute_minimum_eigenvalue(qubit_op)
result_2 = protein_folding_problem.interpret(raw_result=raw_result)
1
2
fig = result_2.get_figure(title="Protein Structure", ticks=False, grid=True)
fig.get_axes()[0].view_init(10, 60)
References
[1] https://en.wikipedia.org/wiki/Levinthal%27s_paradox [2] A.Robert, P.Barkoutsos, S.Woerner and I.Tavernelli, Resource-efficient quantum algorithm for protein folding, NPJ Quantum Information, 2021, https://doi.org/10.1038/s41534-021-00368-4 [3] IUPAC–IUB Commission on Biochemical Nomenclature (1972). "A one-letter notation for aminoacid sequences". Pure and Applied Chemistry. 31 (4): 641–645. doi:10.1351/pac197231040639. PMID 5080161.1
2
3
4
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.2 |
qiskit-aer | 0.12.0 |
qiskit-ibmq-provider | 0.19.2 |
qiskit | 0.39.2 |
qiskit-nature | 0.4.2 |
qiskit-optimization | 0.4.0 |
| System information | |
| Python version | 3.10.6 |
| Python compiler | GCC 11.2.0 |
| Python build | main, Oct 24 2022 16:07:47 |
| OS | Linux |
| CPUs | 128 |
| Memory (Gb) | 2015.6843872070312 |
| Thu Nov 17 07:19:27 2022 +07 | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.